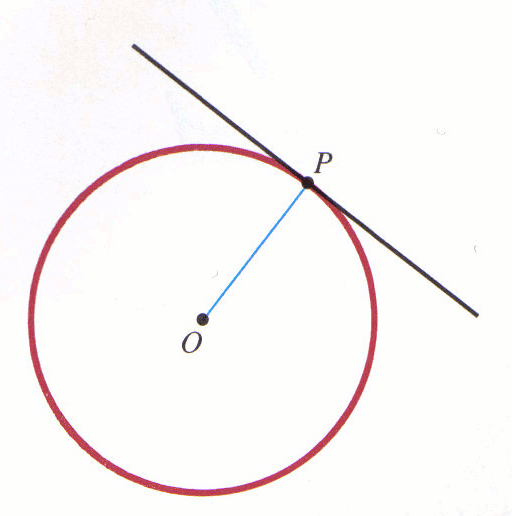
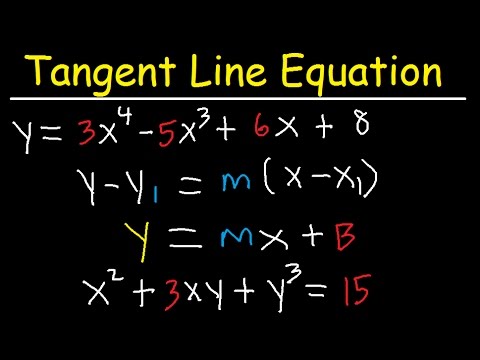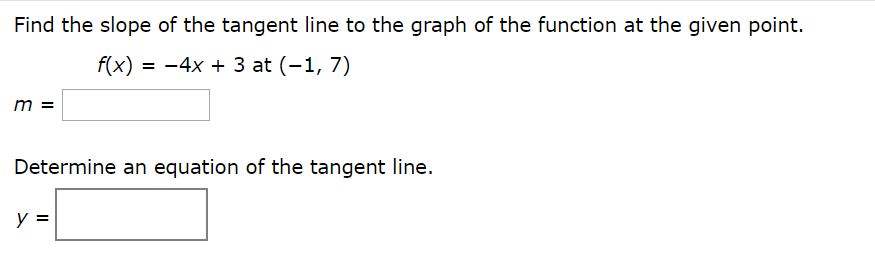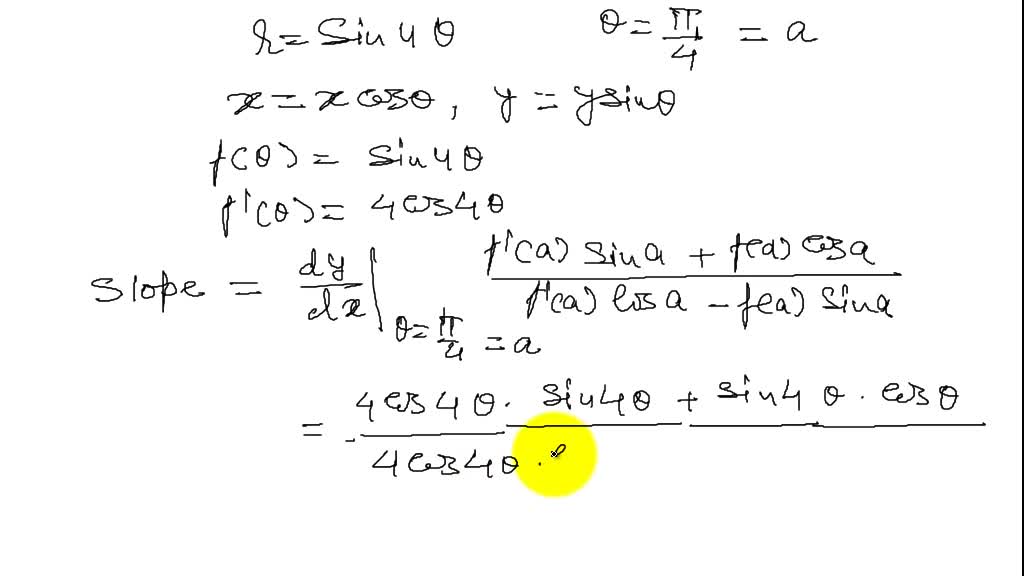Term Definition secant A line that intersects a circle in two points. Tangent A line that intersects a circle in exactly one point. Average rate of change The average rate of change of a function is the change in y coordinates of a function, divided by the change in x coordinates.
Instantaneous rate of change The instantaneous rate of change of a curve at a given point is the slope of the line tangent to the curve at that point. Secant line A secant line is a line that joins two points on a curve. Slope Slope is a measure of the steepness of a line. A line can have positive, negative, zero , or undefined slope.
Together we will walk through three examples and learn how to use the point-slope form to write the equation of tangent lines and normal lines. Thus, equations of the tangents to graphs of all these functions, as well as many others, can be found by the methods of calculus. The formulas above fail when the point is a singular point.
In this case there may be two or more branches of the curve that pass through the point, each branch having its own tangent line. When the point is the origin, the equations of these lines can be found for algebraic curves by factoring the equation formed by eliminating all but the lowest degree terms from the original equation. Since any point can be made the origin by a change of variables this gives a method for finding the tangent lines at any singular point. The geometrical idea of the tangent line as the limit of secant lines serves as the motivation for analytical methods that are used to find tangent lines explicitly.
The question of finding the tangent line to a graph, or the tangent line problem, was one of the central questions leading to the development of calculus in the 17th century. The two tangent lines to the circle are two special solutions. At any other line through the origin, the line intersects the circle at two distinct complex solutions, but at the tangent lines, the two intersection points collide into a double solution. At a double solution, the Jacobian matrix of the system no longer has full rank. Both Apollonius and de Roberval used geometrical methods to construct tangent lines. One of the first algebraic methods is due to René Descartes, one of the inventors of analytic geometry.
It was well known that a tangent line to a circle is always perpendicular to the radius of the circle. So Descartes' idea was to first find a circle tangent to the given curve. Then the tangent to that circle is the sought after tangent to the curve. In geometry, a tangent line to a circle is defined as a line that touches the circle at only one point.
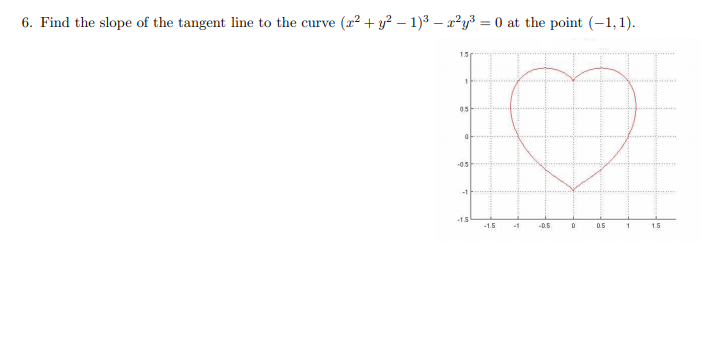
To define, tangent line's slope of a function practicing the calculus method requires differentiation of function with respect to the origin of the line. Simply the derivative of a function at any given point is equal to the tangent slope at that point. I always like solving advanced problems with basic methods.
For example, many problems that we usually think of as "algebra problems" can be solved by creative thinking without algebra; and some "calculus problems" can be solved using only algebra or geometry. Using simple tools for a big job requires more thought than using "the right tool", but that's not a bad thing. I want to look at several ways to find tangents to a parabola without using the derivative, the calculus tool that normally handles this task. To determine the x coordinate of the point of intersection of the two tangent lines, we set the tangent line equations equal to one another and solve for x. As long as mathematicians have been studying curves, they have been interested in the construction of their tangent lines. Apollonius, who lived over two thousand years ago and studied the conic curves extensively, found geometric methods for constructing tangent lines to parabolas, ellipses, and hyperbolas.
In fact, Propositions 33 and 34 of Book I of Apollonius' great work, The Conics, give recipes for constructing tangents to these curves. To find the equation of a tangent line, sketch the function and the tangent line, then take the first derivative to find the equation for the slope. Enter the x value of the point you're investigating into the function, and write the equation in point-slope form. Check your answer by confirming the equation on your graph. Unlike a straight line, a curve's slope constantly changes as you move along the graph.
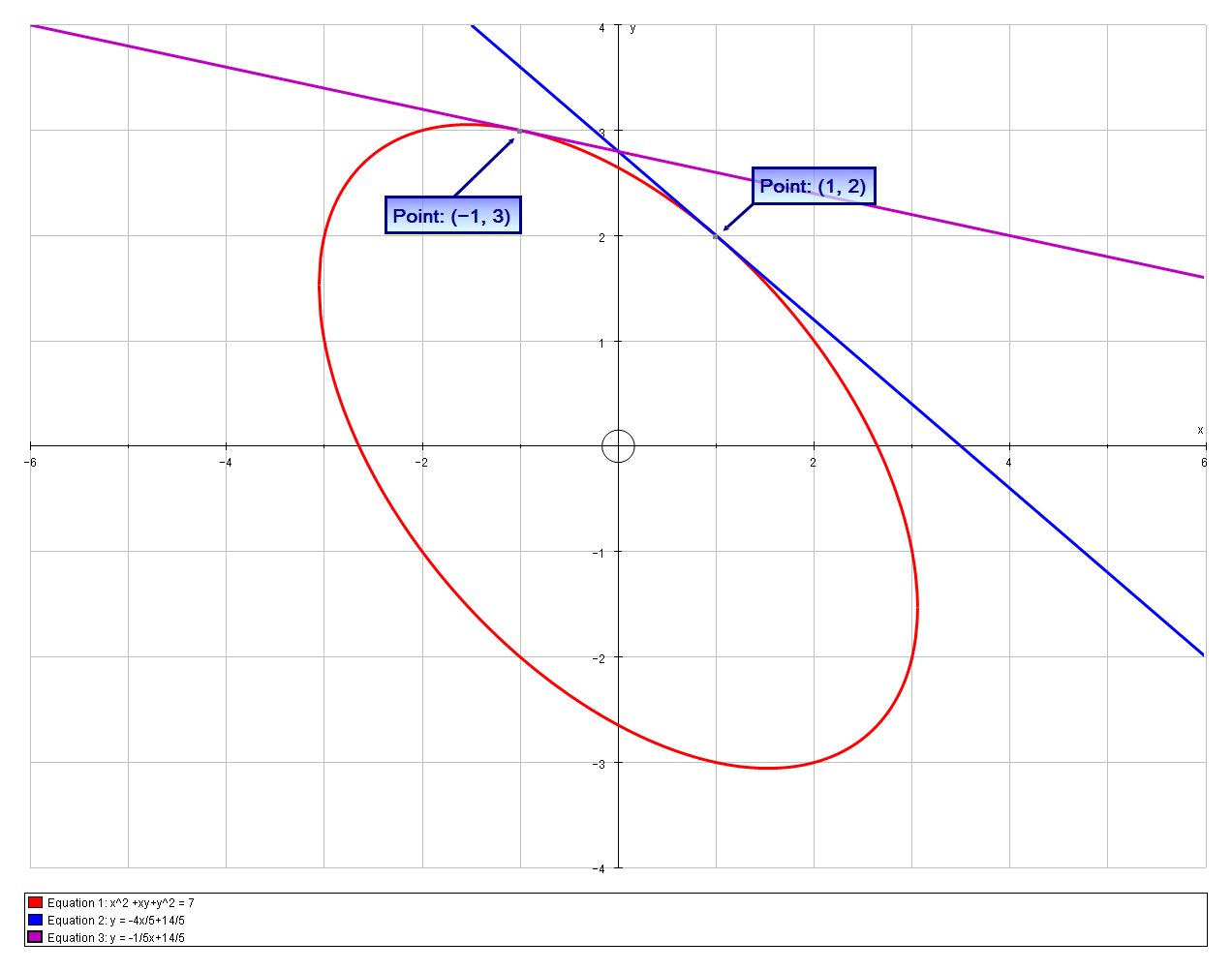
To find the equation for the tangent, you'll need to know how to take the derivative of the original equation. How tangent lines are a limit of secant lines, and where the derivative and rate of change fit into all this. Recall that the roots of this equation represent nothing but the x-coordinates of the points of intersection of the two curves. If the line touches the circle, then the roots of this quadratic equation must be equal, or coincident.
Differentiate the equation of the circle and plug in the values of x,y in the derivative. Use the slope-point form of the line to find the equation, with the slope you obtained earlier and the coordinates of the point. Likewise, we can even extend this concept to writing equations of normal lines, which are also called perpendicular lines. The only difference will be that we will simply use the negative reciprocal slope of the line tangent.
The tangent at A is the limit when point B approximates or tends to A. You can solve this problem without calculus if you know that a tangent is at right angles to the radius at the point of contact. Thus the line from the centre of the circle to the point of cantact of the tangent to the circle is perpendicular to the tangent and thus has slope -1.
With non-negative curvature, arcs of initial circles, and straight line segments tangentially connecting points on these curves. Now to find the slope of line K ideally we will require two points on the line, but we know that the radius and the tangent in a circle are always going to be perpendicular to each other. If two lines are perpendicular, the product of the slopes will always be equal to -1.
I calculate the slope of the tangent line according to the fact that the slop of the tangent line is equal to derivation of the circle at that point. Then I have a point off the circle and the slope and I need to find the point on the circle. So I have 2 equations and two unknown variables which are and by solving them I get . This is not a MATLAB question - it's just analytical geometry formulas and algebra. Just draw it out and make sure you see the right angle between the center, the point off the circle, and the point on the circle. Power transmission – Two circles joined by a pair of mutual tangents can be used to solve the problem of belt length over pulleys.
The sum of the length of tangent lines and the arc subtended by them can be used to find the length of the belt. Apollonius' recipes for constructing tangent lines to conic curves are easy to implement, but his methods were limited in that they could only be applied to a handful of curves. Of course, in the days of antiquity, there weren't that many curves that people were interested in studying, and so there wasn't that much of a need for a general method. Learn how to solve systems of linear equations by graphing. After reviewing linear equations, see examples of solving systems of two equations by graphing. Point-slope form is a form of a linear equation where there are three characteristic numbers - two coordinates of a point on the line, and the slope of the line.
Review the definition of the point-slope form of a linear equation and other forms of writing a linear equation with a few examples. Find the equation of the tangent line to the circle with center at the origin, at point . Find the equation of the tangent line to the circle with center at (-3,1), at point (-2,5). Also, do not worry about how I got the exact or approximate slopes.
We'll be computing the approximate slopes shortly and we'll be able to compute the exact slope in a few sections. Therefore, let's formally lay out the steps for writing the tangent line equation to a curve, as this particular skill is pivotal for future lessons dealing with linearization and differentials. Because if we are ever asked to solve problems involving the slope of a tangent line, all we need are the same skills we learned back in algebra for writing equations of lines.
The first step is to determine a general formula for the slope of a tangent to the given circle. What is the equation for the slope of a line tangent to the circle? Click the "Submit" button after selecting your answer.
These methods led to the development of differential calculus in the 17th century. Further developments included those of John Wallis and Isaac Barrow, leading to the theory of Isaac Newton and Gottfried Leibniz. Here I have constructed part of a parabola with the given focus and directrix; for point P I have shown the segments PF to the focus and PQ to the directrix, both with the same length a. In the second step I will be showing that line PM, joining P and the midpoint M of FQ, is tangent to the parabola; for now, it's enough that it looks right.
We have an incoming light ray parallel to the axis and perpendicular to the directrix, so it is collinear with PQ. It strikes the parabola at 'angle 1', which is congruent to angle QPM. But angle QPM is congruent to angle FPM, 'angle 2', since PM is the median of isosceles triangle FPQ and consequently also the angle bisector. Therefore 'angle 2' is the direction in which the light will exit, passing through the focus. Now we have a circle that is tangent to the parabola.
We haven't yet found the slope of the tangent line. To do that without calculus, we can use the fact that any tangent to a circle is perpendicular to the radius. The radius \(\overline\) has slope -2; so the slope of our tangent line is the negative reciprocal, 1/2. Note that the order of the equations is important.
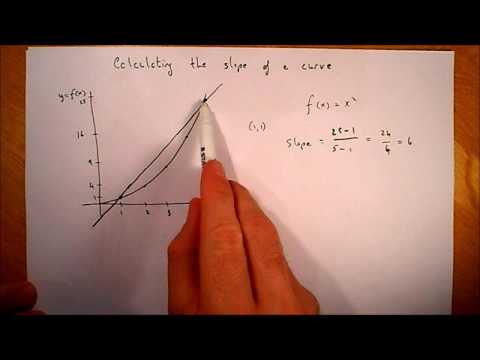
The linear equations that cut down the positive dimensional solutions to isolated points must occur at the end of the list of polynomials. In this exercise you will use de Roberval's method to construct tangent lines to several curves. The right side of this equation is called the difference quotient. The denominator h is the change in x, and the numerator is the change in y. The beauty of this procedure is that more and more accurate approximations of the slope of the tangent line are obtained by choosing points closer and closer to the point of tangency. Tangent line calculator is a free online tool that gives the slope and the equation of the tangent line.
BYJU'S online tangent line calculator tool makes the calculations faster and easier where it displays the output in a fraction of seconds. To calculate the slope of a line or line segment, an imaginary triangle known as a slope triangle is used. Understand the definition and concept of a slope triangle, and examine slope triangles, graphs, and negative slope.
In this lesson, learn to define and write equations for horizontal and vertical lines. Moreover, learn to graph and find slope of horizontal and vertical lines. In mathematics, fractions can be challenging, but it is possible to make them easier. Review the simplification steps, and practice examples to understand how to make negative fractions easier to solve. Understand what a slope-intercept form is by its definition and know its importance. Learn its formula and how to graph it through the given examples.
Find the length of the radius of a circle with center at 4,2 and a point on the circle at -8,6. Determine the coordinates of the other endpoint of its diameter. A circle in quadrant II is tangent to both axes. Find the coordinates of the center of the circle. Many calculus books will treat this as its own problem. We however, like to think of this as a special case of the rate of change problem.
In the velocity problem we are given a position function of an object, \(f\left( t \right)\), that gives the position of an object at time \(t\). Then to compute the instantaneous velocity of the object we just need to recall that the velocity is nothing more than the rate at which the position is changing. In reality there probably won't be 15 cm3 more air in the balloon after an hour. The rate at which the volume is changing is generally not constant so we can't make any real determination as to what the volume will be in another hour.
As with the tangent line problem all that we're going to be able to do at this point is to estimate the rate of change. So, let's continue with the examples above and think of \(f\left( x \right)\) as something that is changing in time and \(x\) being the time measurement. Again, \(x\) doesn't have to represent time but it will make the explanation a little easier. While we can't compute the instantaneous rate of change at this point we can find the average rate of change. This result is the equation of the tangent line to the given function at the given point.
When we have a function that isn't defined explicitly for ??? We can use the point-slope formula to determine the equation of the tangent line. The angle between two curves at a point where they intersect is defined as the angle between their tangent lines at that point. More specifically, two curves are said to be tangent at a point if they have the same tangent at a point, and orthogonal if their tangent lines are orthogonal. At most points, the tangent touches the curve without crossing it .
A point where the tangent crosses the curve is called an inflection point. The slope of the tangent line can be determined by finding the negative reciprocal of this. In other words, flip the fraction and change the sign.
But that's not the final answer because we're trying to find the slope of the tangent line. Since the tangent line is perpendicular to the radius, we can find it by taking the negative reciprocal of the slope of the radius. Finding the negative reciprocal just means that we flip it over and change the sign. A few things have been left unsaid in this lesson – the equation of the tangent in slope form to the circle whose center is not at origin, and the point where the tangent will touch the circle. Unlimited random practice problems and answers with built-in Step-by-step solutions. Practice online or make a printable study sheet.